■ 2要因分散分析の事後の分析 (Post hoc analysis)
- 事後の検定力分析では、効果量をきちんと計算してから行う場合と、J.Cohenが示した慣例(convention)にしたがって、効果量小(Small) f=0.10、効果量中(Medium) f=0.25、効果量大(Large) f=0.40、という数値のどれかを入れて概略的に検定力を算出する場合とがあります。
先の事前の分析で用いた例を再び取り上げてみます。すなわち、「要因A:年代1,2,3,4,5」(df=(5-1)=4)と「要因B:地域1,2,3」(df=(3-1)=2) で不安耐性について、例えば、年代×地域=5x3=15個のグループ(cell セル)のデータ数(Sample size)がすべて20人だったという場合で、全データ数(Total sample size)は15x20=300となります。
このように研究が行われた場合、「事後 post hoc」に、要因A「年代」の検定力を算出してみます。
- [Test family] F tests
- [Statistical test] ANOVA] Fixed effects,special, main effects and interactions
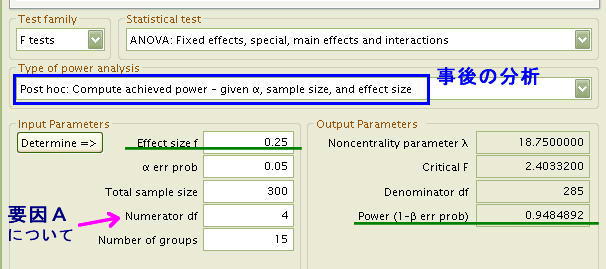
- [Type of power analysis] Post hoc: Comute achieved power - given α, sample size, and effect size
Input Parameters
- [Effect size f] 0.25
(実測値を用いず「効果量は中くらい」だと想定した)
- [α err prob] 0.05 (有意水準は5%)
- [Total sample size] 300 (全データ数 5x3x 20名)
- [Numerator df] 4 (要因A「年代」の自由度df= 5-1 )
- [Number of groups] 15 (グループの総数 5x3)
この結果は下の図をご覧下さい。
Output Parameters
- [Noncentrality parameter λ] 18.7500000 (非心分布のλパラメータの値
- [Critical F] 2.4033200 (5%水準で有意となるためのF値)
- [Denominator df] 285 (誤差の自由度: (20-1)x15グループ=285)
- [Power (1-β err porb)] 0.9484892
|
これにより「要因A:年代(5水準)」についての有意性検定の検定力は「0.9484」と極めて高いことが計算されました。
- 2要因分散分析の事後の検定力分析に実際の効果量を用いる。
ところで、研究が終わった後では、「効果量 中 f=0.25」と勝手に入れてみるのではなく、実際のデータに基づいた効果量(Effect size)を入力して正確な検定力を知りたいわけです。
- 2要因分散分析の事後の検定力分析を「分散分析表」を用いて実施する。
(編集中…)
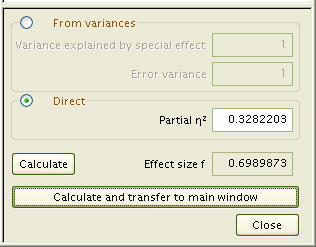
- 事後の検定力分析では「効果量 f 」の数値が必要となります。G*Powerソフトでは、[Determine]というボタンをクリックすると、効果量 f を求めるための計算パネルが右側に表示されます。入力数値としては2種類の入力方法が選べます。
- From variances
Variance explained by special effect [ ]
- σ2m (要因の標準偏差の二乗)↑
Error variance [ ]
- σ2 (全体の標準偏差の二乗)↑
- Direct
Partial η2 [ ]
- 偏相関係数 ↑
[Calculate] Effect size f [ ]
- 計算させると効果量 f が表示される↑
|
|
- 上の右側にある「効果量の計算パネル」では、分散の二つの数値を入れるか、偏相関係数を一つ入れるかして、効果量を計算します。一元配置や二元配置の分散分析までは、σやσmの計算もそれほど難しくなくできますが、3要因分散分析となると、一次の主効果(A,B,C)、二次の交互作用(AxB,AxC,BxC)、三次の交互作用(AxBxC)となりかなり面倒なことになります。
3要因分散分析については、G*Powerのサイトには詳細な説明があったので、どのくらい面倒かを実際に確認してみましたが、「効果量の計算パネル」に入れる分散の数値について理解するのに役立ちました。
以下は要因A(3水準)、要因B(3水準)、要因C(4水準)の分散分析(各セル内の度数は 3 )において、36個のセルにおける平均値(m)・標準偏差(s)・セル内データ数(n)のリストです。
表1
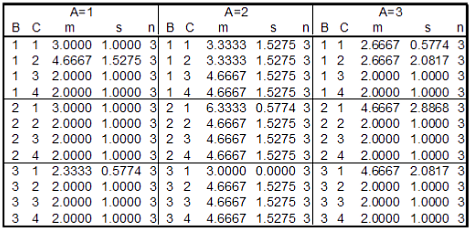
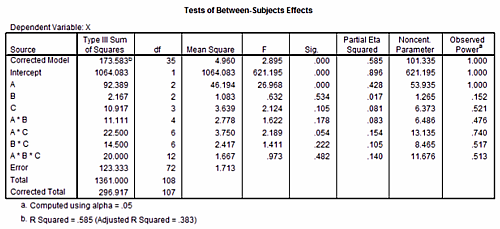
この仮想データについて3要因の分散分析をSPSSソフトのGLM (一般線形モデル)で分析した際の分散分析表が掲載されおり、その内容をG*Powerソフトであらためて確認することで、どのような数値を用いるかなど、使い方の説明となっています。
(G*Powerでは母数をパラメータとして用いるので、標本統計量を用いているSPSSとは、η2 の数値が異なりますが、その変換式も説明されています。なお、結果として得られる検定力そのものの数値はどちらも同一となっています。)
- 表1をデータとする3要因分散分析の検定力分析の内容を以下にまとめておきます。
●元の英文の内容は → G*Powerの解説(英文+図表) をご覧ください)
●参考のため、数値と計算について数表を作成しました → [Excel数表]
- (「読み取り専用」をクリックしてください)
要因A、B、Cの主効果
- 36個の平均値の平均を求めることで「全体平均値」を算出します。
全体の平均値 mg (grand mean) = 3.1382
- 共通の分散 σ2 は36個の各セルの標準偏差 s をそれぞれ二乗して合計したものの平均値です。
共通の分散 σ2 = 1.71296 ( σ2= 1/36 Σi Si2)
次に要因A、B、C、それぞれの主効果を求めます。
- 要因Aの三つの平均値、μ1 * * μ2 * * μ3 * * は次の数値です。
なお、三つの平均値からそれぞれ全体平均( mg )を差し引いた数値にしてあります(合計が0)。
μi * * = { -0.722231, 1.30556, -0.583331 }
それぞれを二乗してその平均値 σA2を求めます。
σA2 = ( (-0.722231)2 + (1.30556)2 + (-0.583331)2 ) / 3
σA2= 0.85546
要因Aの効果量は fA = √ ( σA2 / σ ) なので…
fA = √ ( 0.85546 / 1.71296 ) = 0.7066856
- 同様にして
要因Bの三つの平均値 μ* j * = { -0.0555556, 0.19444444, -0.1388889 } から
σB2= 0.02006173
したがって要因Bの効果量は fB = √ ( 0.02006173 / 1.71296 ) = 0.10822379
また
要因Cの四つの平均値 μ* * k = { 0.52776944, -0.027775, -0.2499972, -0.2499972 } から
σC2= 0.10107731
したがって要因Cの効果量は fC = √ ( 0.10107731 / 1.71296 ) = 0.2429212
- ねんのため、それぞれの偏相関係数 η2を計算してみます。η2 = f2 / ( 1 + f2) の式を用います。
- ηA2 = fA2 / ( 1 + fA2) = 0.33308116
- ηB2 = fB2 / ( 1 + fB2) = 0.0115768
- ηC2 = fC2 / ( 1 + fC2) = 0.05572249
G*Powerの効果量計算パネルには、ここで示した数値を入力することで効果量を計算してくれるわけです。「 From variances」の「variance explained by special eefect」の欄には σAやσB、あるいは σCを入れて、その下の欄の「Error variance」には σ を入れる―。
または、「 Direct」の偏相関係数 「Partial η2」にそれぞれの偏相関係数 ηA2 、ηB2 、 ηC2 を入れることができます。
(ここではすでに効果量 f は計算済みなので、効果量計算用のパネルを用いる必要はありませんが、使い方の解説をしています。)
以下は要因Aについて検定力を求めた場合のG*Powerの画面、および「効果量計算パネル」です。
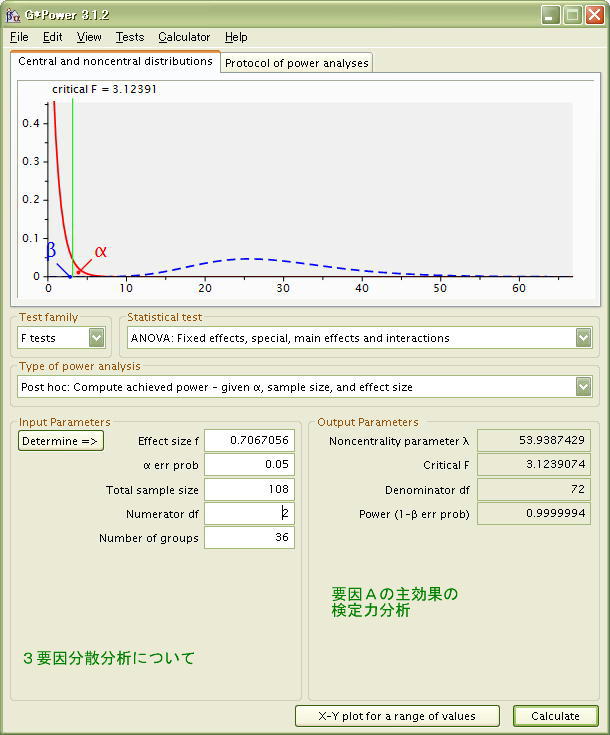
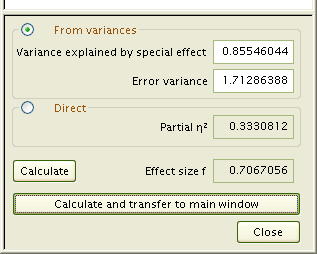
このように要因Aは、 検定力 (1-β)は 0.9999994 と極めて高いことが分かりました。
なお、要因Bについては (1-β)= 0.1519503、また要因Cについては (1-β)= 0.5208786 となります。G*Powerで確認してみてください。
要因Bの検定力はかなり低く、36個のセルに各3名(回)のデータを用いてこの研究では要因Bの効果を把握できていないことが分かります(分散分析でも有意になっていませんし)。また、要因Cの検定力も0.52...と低く、こちらも不十分なことが分かります (ダミーのデータですが…)。ただし、36個のセルに各3名(回)と少ないデータ数にも関わらず、要因Aの効果は、検定力の高さもあいまって十分に確認されたことになります。したがって、この研究がもっぱら要因Aの効果に注目して計画された研究だったならば、とりあえず当初の目的は達成したことになるでしょう。
2要因交互作用 AxB、AxC、 BxC
-
2要因の交互作用についても検定力分析に必要なのは σAxB 、 σAxC 、 σBxC という標準偏差の数値です。この数値は「2要因交互作用における残差 residual」と呼ばれ次の式で表されます。ここでは、AxBの交互作用 δi j *について説明を進めます。i で要因Aの水準を表し、 j で要因Bの水準を表し、 k で要因C の水準を表しています。アスタリスク * は、それぞれの要因の部分の水準をすべて含む (水準の違いを問わない) ことを意味しています。
- 要因AとBの交互作用を表す残差の式 δi j * = μi j * - μi * * - μ* j *
μi j *は、要因Aと要因Bの3行3列、9個あるそれぞれの平均値。
μi * *は、要因Aの3個あるそれぞれの平均値。
μ* j *は、要因Bの3個あるそれぞれの平均値、をそれぞれ指しています。
要因Aは3水準( i =1,2,3 )、要因Bも3水準( j=1,2,3 ) なので、残差は次の9個となります。
{ δ11* δ12* δ13* δ21* δ22* δ23* δ31* δ32* δ33* }
{ 0.555564, -0.351111, -0.194453, -0.388903, 0.444447, -0.055444, -0.166661, -.0.0833361, 0.249997 }
求める σ2AxB は、この9個の値をそれぞれ二乗して合計した数値の平均値です。したがって
σ2AxB = ( (0.555564>2 + (-0.351111)2 + (-0.194453)2 + (-0.388903)2 + (0.444447)2 + (-0.055444)2 + (-0.166661)2 + (-.0.0833361)2 + (0.249997)2 ) / 9
σ2AxB = 0.102881 となりました。これを分子にして効果量 f を計算します。
- (なお、分母となる σ2= 1.71296 は上で計算済みです。)
この二つをG*Powerの効果量計算パネルに入れると、以下のように偏相関係数 η2と効果量が計算されます。
[variance explained by special effect (特殊効果によって説明された分散)] には σ2AxB = 0.102881 を入力し、
[Error variance (誤差分散)] には σ2 = 1.71296 を入れて[Calculate]をクリックすると計算されます。
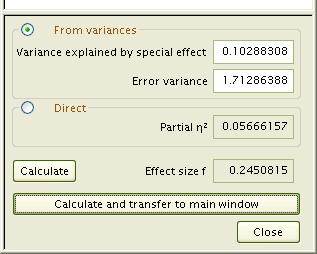 |
なお、
要因AxBの2要因交互作用の効果量
- fAxB = √ ( 0.102881 / 1.71296 ) = 0.2450815
もちろん、すでに効果量 f は計算済みなので、G*Powerのメイン画面の入力欄に直接入力してもokです。
要因AとBの交互作用の偏相関係数についても
η2AxB = f 2AxB / ( 1 + f 2AxB ) の式に基づいて、
η2AxB = 0.2450722 / (1 + 0.2450722 ) = 0.05666157 となることも確認できます。
|
次の図は、G*Powerのメイン画面の設定内容です。
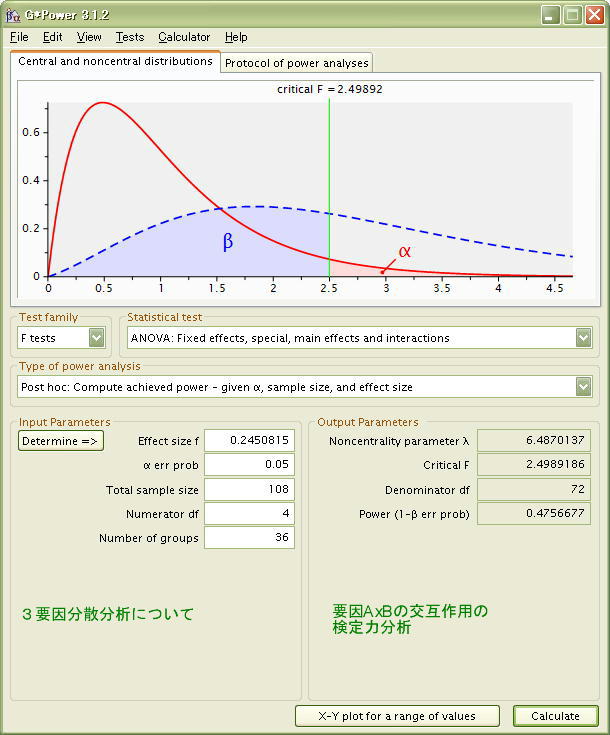
要因AxBの相互作用の自由度は Numerator df = 4 です。これは (要因Aの水準数 - 1 ) x (要因Bの水準数 - 1) = 2 x 2 =4 です。
事後の検定力分析の結果、AxBの交互作用の検定力は Power = 0.4756677 と、あまり高くないことが確認されました。
同様な計算によって、 AxC の交互作用の検定力 Power = 0.7402635 とある程度の高さがあることが分かります。またBxC の交互作用の検定力 Power = 0.5166079 となり、あまり検定力が高くないことが分かります。詳しい内容は計算用の数表をご覧ください。
3要因A、B、C の 交互作用
-
さて、いよいよ3要因A、B、C の交互作用について、その検定力を計算することになります。計算の基本的な考え方は前と同じで、交互作用の残差δi j k を計算して、それから 効果量を計算するための σ i j k2 を求めます。
3要因の残差 δi j k は次の式で表されます。
- δi j k = μi j k - μi * * - μ* j * - μ* * k - δi j * - δi * k - δ* j k
-
μi j k はセル(i,j,k)の平均値
μi * * は、要因A(水準 i = 1,2,3) の三つの平均値
μ* j * は、要因B(水準 j = 1,2,3) の三つの平均値
μ* * k は、要因C (水準 k = 1,2,3,4) の四つの平均値
δi j * は、要因AxBの9個の残差 (i = 1,2,3 と j = 1,2,3 の組み合わせによる)
δi * k は、要因AxC の12個の残差 (i = 1,2,3 と k = 1,2,3,4 の組み合わせによる)
δ* j k は、要因BxC の12個の残差 (j = 1,2,3 と k = 1,2,3,4 の組み合わせによる)
要因AxBxC の水準 3x3x4 = 36個のセルがあるので、3要因の交互作用を示す残差 δi j k は36個の要素からなります。
-
| | A=1 | A=2 | A=3 |
| B | C | δ(1jk) | δ(2jk) | δ(3jk) |
| 1 | 1 | 0.33333611 | 0.16666944 | -0.5000056 |
| 1 | 2 | 0.77779167 | -0.944475 | 0.16668333 |
| 1 | 3 | -0.5555639 | 0.38890278 | 0.16666111 |
| 1 | 4 | -0.5555639 | 0.38890278 | 0.16666111 |
| 2 | 1 | -0.4166556 | 0.66665278 | -0.2499972 |
| 2 | 2 | -0.3055667 | 0.22224167 | 0.083325 |
| 2 | 3 | 0.36111111 | -0.4444472 | 0.08333611 |
| 2 | 4 | 0.36111111 | -0.4444472 | 0.08333611 |
| 3 | 1 | 0.08331944 | -0.8333222 | 0.75000278 |
| 3 | 2 | -0.472225 | 0.72223333 | -0.2500083 |
| 3 | 3 | 0.19445278 | 0.05554444 | -0.2499972 |
| 3 | 4 | 0.19445278 | 0.05554444 | -0.2499972 |
|
この36個の残差を二乗して合計します。
その平均値がσ2AxBxC となります。
- σ2AxBxC = 0.185189
なお、数式は以下の通りです。
σ2AxBxC = 1 / 36 Σ i,j,k δ2i j k
|
-
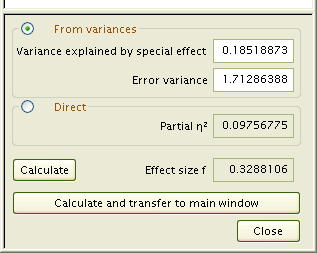
|
計算したσ2AxBxCを分子にして、分母はσ2 = 1.71296 にして
効果量 f を計算パネルで計算させます。
効果量 f = 0.3288016 となり、
偏相関係数 η2AxBxC = 0.09756294
と計算されました。
この効果量をメインパネルに転送(transfer)して
検定力 Power (1-β)がどの程度がを計算します。
|
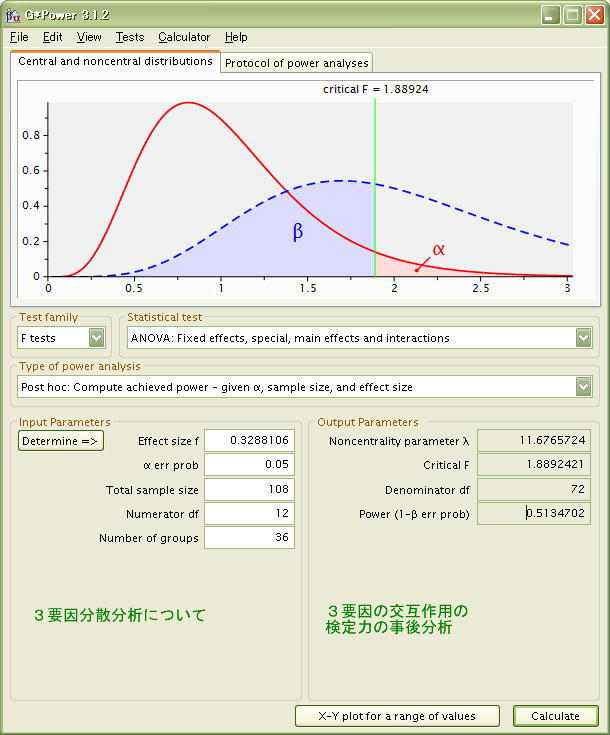
検定力 Power =0.5134.. とそれほど高くはないけれども、ひどく低い数値ではないことが分かりました。3要因の交互作用の検定力を高めるためには、とりあえず、36個のセルの各データ数が[3]と低いことから、データ数をそれぞれ 4〜以上として、測定の回数・度数を増やしたら検定力がより高くなることが考えられるわけです。
以上が、3要因分散分析における検定力分析の実際でした。要因A,B,C の三つの要因の主効果、要因AxB, BxC, AxC の2要因交互作用、そして、要因AxBxC の3要因の交互作用 を計算することで必要な数値を算出しました。
なお、SPSSのGLM (一般線型モデル)で分散分析した場合の検定力の数値は、ここで示した結果と同じです。したがって、実際にはSPSSの結果をそのまま用いれば良いことになります。注意点としては、SPSSでは標本統計量を用いていることから、G*Powerとは偏相関比の数値が異なることです (変換式が示されています)
また、「対応のあるデータについての分散分析」といえる「反復測定の分散分析」(ANOVA: repeated measures) については次に説明していくことにします。
( G*Power の論文に記載されています → [G*Power 2007] )
|