対応のあるデータのt検定とG^*Power

■ 対応のあるデータのt検定とG^*Powerの設定例

この参考例は、以下のサイトに基づいています。

[ How to use GPower ] (英語)
※上のサイトは宗教的な内容を含むサイトにありますが、G^*Powerの設定の１〜５４の全て(Exact, F tests, t tests, χ2tests, Z tests)について網羅していること、それぞれについての設定例をYouTube動画で説明しているため、敢えてリンクをしています。また動画は英語文の解説のみでトークはなくコンパクトで使いやすいこともその理由です。


●対応あるデータについての「平均値の差のt検定」
　「対応あるデータ」とは、一人の被検者にある検査を行い、その後、何らかの処置・対処(投薬や作業など)を行った後に、もう一度調べてみる…という場面を想定しています。その場合、Ａさんのデータの1回目、2回目、Ｂさんのデータの1回目、2回目、Ｃさんのデータの1回目、2回目…のデータが得られますが、元々、最初の検査で低かった人や、最初から検査で高い数値を出した人がいるため、個々の被検者についての「効果」を調べるためには、グループ全体の平均値を対比してもあまり意味がないことになります。
　こうした場面に登場するのが、「対応のあるデータ」についての「t検定」です。
　なお、三回以上測定する場合は、「対応のあるデータ」についての「(反復測定)分散分析」を用いる必要があります。
　
ビデオ動画はこちら→ 対応のあるt検定のG^*Powerの設定例

---

　〜　解説　A prior: 必要なケース数の事前の検討〜

---

15. 二つの対応のあるデータのt検定

Means: Difference between 2 dependent groups
(Compute power and sample size for a paired [within, correlated, dependent] or matched samples t-test.)
対になった[被験者内、相関のある、従属的］あるいは対応のある標本のt検定

例：
抗うつ剤を処方された被検者の気分状態についての変化を検出するためには何人ほど被検者が必要とされるだろうか？

抗うつ剤を服用する前の被検者での、気分状態の期待平均が46(期待される標準偏差は 5.1)とする。
抗うつ剤を服用後の同じ被検者の気分状態の期待平均が50(期待される標準偏差は5.8)とする。
※メモ　「対応するペア」の実験デザイン
　そこでは、双方のグループ内の被検者は異なっているが、被検者はある特性においてペアとなっていて、その手続きは同一である。

[Tail] (片側検定では)"1"を入れるか、(両側検定では)"2"を入れる。ここでは"2"を入れて両側検定とする。事後の数値が事前の数値と比べて高いかあるいは低いときは"2"を入れ、それ以外の場合は"1"を入れる。

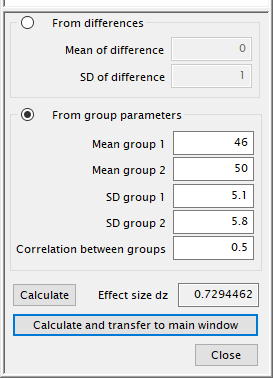
[Effect Size dz]については、 [Determine]をクリックして(副画面を表示させて)
[From group parameters]を選択する。
group1 には予想される平均値として"46"を入れ、group2には"50"を入れる。
group1 の予想される標準偏差として"5.1"を入れ、group22は"5.8"を入れる。
二つのデータ間の予想される相関を入れる。ペアにしたデータを分析しているので、穏当な数値から高めの数値、例えば"0.50"などとする。

[Calculate] をクリックして[Effect size dz]を計算させると "0.7294..." と算出されたので、[Calculate and transfer to main window]をクリックして、主画面に効果量dzの数値を転送する。

[α err prob]　すなわち、「Type I エラー」の数値は、"0.05"か"0.01"を入れる。
ここでは(5%水準として) "0.05"を入れる。
[Power (1-β err prob)] の効果量には、(通常は80%かそれ以上)として"0.80"を入れる。
[Calculate]をクリックして、必要データ数を求めると、[Total sample size]は"17"(人)となる。



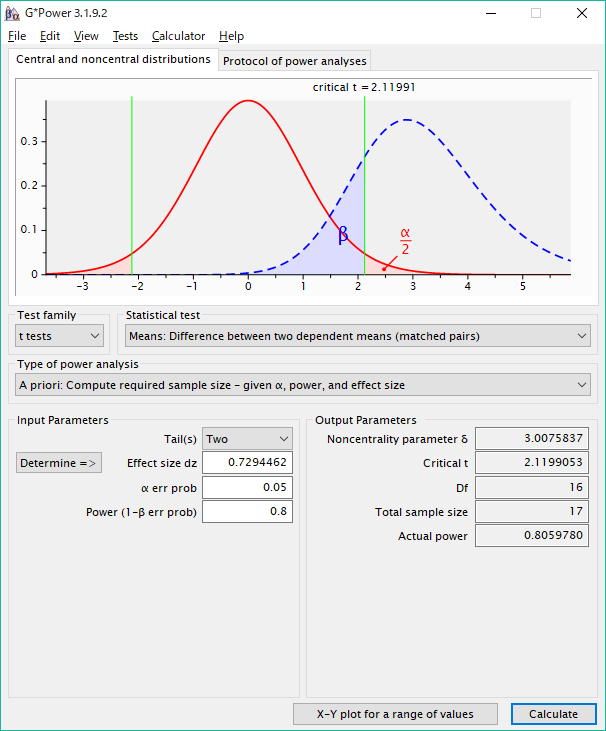
ここでは期待する検定力の度合いとして"0.8"(Cohenが示した慣例値)を用いていますが、
さらに小さく、例えば"0.60"とすると、必要とされるデータ数は減少して12人となります。
※Cohenは「検定力が0.70位でも、それなりに意味がある」と述べているので、それをさらに進めて"0.60"…。

　この例は、事前に「抗うつ剤投与」の前後でどのような数値になるか、ある程度の目安があるとして
投与前後の平均値を(勝手に)入れている状態です。
　仮に、投与前後であまり大きな変化がないことが予想されるのならば、group1(事前)の平均値を"46"として、
　group2(事後)の平均値を"47.5"などと想定して必要なデータ数を求めてみると(それ以外は前のままの設定)、
検定力の想定が"0.60"と緩い場合でも、何と68人の被検者が必要となります。
このように平均値に様々な数値を入れてみることで、抗うつ剤の投与の効果が高く見込めない場合は、
被検者数をある程度確保しておくという実際的対応が必要となります。


---------原文-------------------------------------------------

15. Means: Difference between 2 dependent groups

(Compute power and sample size for a paired [within, correlated, dependent] or matched samples t-test.)
Example: How many participants are needed to detect a change in mood states for participants who are given an antidepressant?
The expected average mood state in participants prior to taking an antidepressant is 46 (expected standard deviation = 5.1).
The expected average mood state in the same participants after taking an antidepressant is 50 (expected standard deviation = 5.8).
(Note: in a matched pair design where the participants in both groups are different, but they are paired on certain characteristics, the procedure is the same).

Tails = 1 or 2 tails (choose 2 tail if the post-treatment score could be higher or lower than the pre-treatment score, otherwise choose 1 tail).
Effect Size dz = Click “determine” and select “From group parameters”.
Enter expected means for groups 1 (46) and 2 (50).
Enter expected standard deviations for groups 1 (5.1) and 2 (5.8).
Enter expected correlation between the 2 sets of data. Should be moderate to high in a paired samples scenario (e.g., 0.5).
Calculate effect size and transfer to main window.
α err prob = choose a Type I error rate (0.05 or 0.01)
Power = select a desired level (usually 80% or higher)

Video:
https://www.youtube.com/watch?v=qIxuLRUSRf4
-------------------------------------------------------------