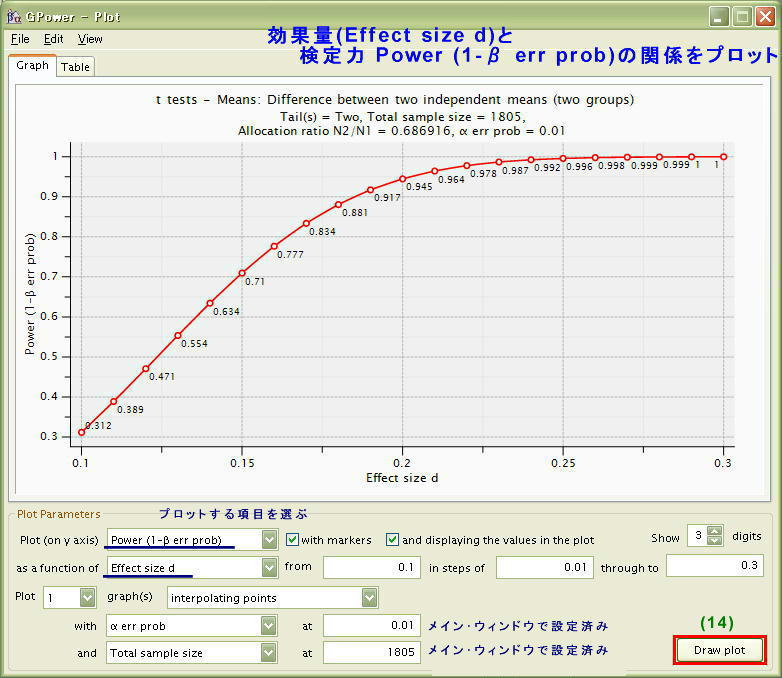
|
[追加2/21, 更新3/10, 2011]
[平均値の差の t 検定]の検定力分析について

|
■ 「平均値の差のt 検定」 事前の分析 (A Priori analysis)
- 「平均値の差のt検定」の検定力については、J.Cohenの表1、表2の解説のところで基本的な内容を扱っています。そちらもご覧ください。
●下のG*Powerの画面は「二つの異なるグループの平均値の差の t 検定」について、「事前の検定力分析 A priori Power analysis」によって、二つのグループそれぞれに必要なデータ数 (sample size)を算出するための画面です。
* この画面はG*Power3.0の古いバージョンです。残りの表示はすべてVersion 3.1.2で示します。
G*Powerの画面の中の[赤い四角の枠]の部分をクリックすると説明が一番下の欄に表示されます。
- 「説明欄」の表示をリフレッシュするときはクリックしてください→[表示のリフレッシュ]
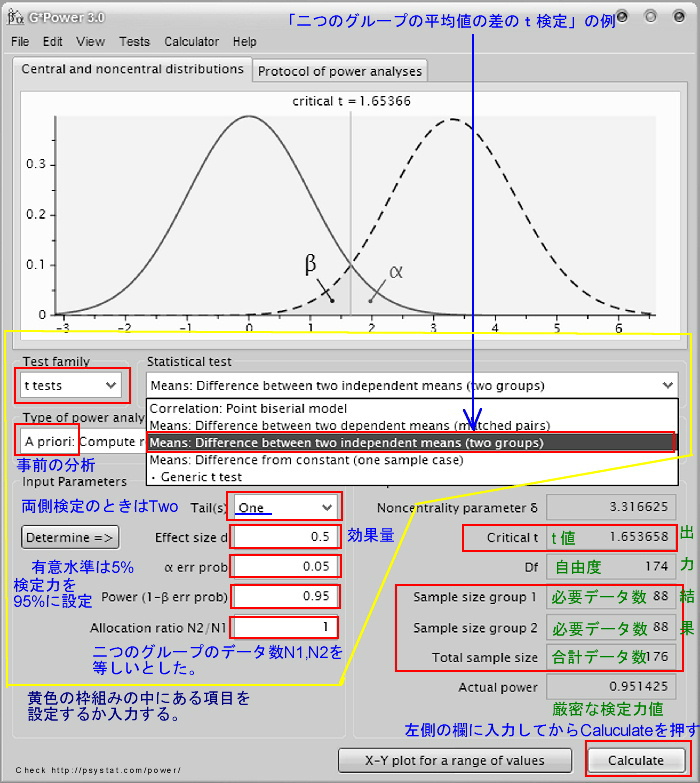
上の図の例では、「片側検定」「有意水準 5%」「検定力 0.95と高く設定」「二つのグループのデータ数は同じと設定」した場合、一つのグループのデータ数は88で、二グループで176個のデータが必要だということが分かりました。
|
■ 「平均値の差のt 検定」 事後の分析 (Post hoc analysis)
すでに実施した研究のt 検定がどの程度の検定力(statistical power)をもつかを事後に計算します。
有意性検定の結果をどの程度主張することができるのかを確認します。
*なお、用いた数値データは院生のM.Y.さんから提供されたものです。M.Y.さんの研究をきっかけにこの「検定力分析のすすめ」のサイトを作成することになりました。記して感謝いたします!
G*Power画面上に示した番号順に[赤い四角の枠]をクリックしてみてください。
説明が一番下の「説明欄」に表示されます。
「説明欄」の表示をリフレッシュするときはクリックしてください→[表示のリフレッシュ]
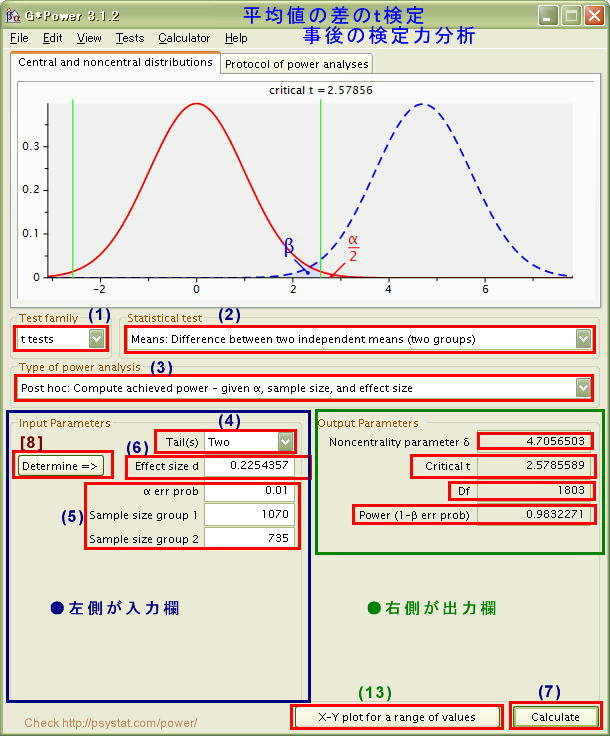
- 以上のようにして、研究で用いた「平均値の差のt検定」がどの程度の検定力をもっているかを
あらためて事後に確認することができました。
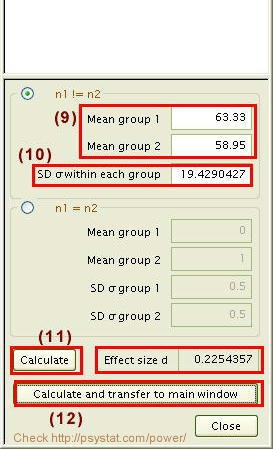
なお、検定力Power=0.98 というのは極めて高い数値です。こうした数値が実現できたのは、ひとえにデータ数が1000の大台にのるほど大きかったためといえるでしょう。ちなみに、効果量は d =0.22 程度と「小(Small)=0.2」よりも少し大きいだけです。したがって、平均値の差は「5」くらいと一見して大きな差には見えないかもしれませんが( m1=63.33、 m2=58.95)、実質的な差があると言うことができるでしょう。
* なお、J.Cohenは「検定力 Power=0.8」を検定が有効であるための基準として提案しています。
これよりも小さな検定力、例えば「Power=0.6〜0.5」ならば、β過誤(証明したい対立仮説
を採択しないでいる確率)が 0.4〜0.5と大きくなりすぎること。また、0.8よりも大きな検定力、
例えば「Power=0.9」などではβ過誤=0.1と小さくなるのですが、それを実現するためには大量の
サンプルが必要となる可能性があるため、一つの目安として 「Power=0.8」を唱えています。
なお、Power=0.7程度の数値もそれなりの検定力がある(β過誤= 0.3)と述べています。
|
- 「平均値の差のt 検定」では、効果量d の数値として慣例となっている「効果量 小(Small)=0.2」か「効果量 中(Medium)=0.5」か「効果量 大(Large)=0.8」を入力しても良いのですが、すでに研究を終えているので研究結果である実際の数値を用いて、正確な効果量d の値を計算することができます。
メイン・ウィンドウの[Determine =>]をクリックすると、右のような「効果量の計算パネル」が表示されます。→
ここに二つの平均値を入力します。
なお、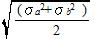
グループ1の標準偏差σ1は 20.27
グループ2の標準偏差σ2は 18.56
なので、σを手計算して入力します。
σ=√ [[(20.27)x(20.27)+(18.56)x(18.56)]/2]
= 19.4290427
計算した結果をメイン・ウィンドウの「効果量 Effect size d」に転送します。
そのようにして正確な効果量を決めてから、求める「検定力」を算出します。
|
◎効果量dの正確な数値を割り出す
計算パネル
|