「相関」の検定力分析
- 二変数の関連性を調べる指標として、ピアソンの偏差積率相関係数 (二つの変数がいずれも実数値をとる場合に用いる通常の相関係数) がよく用いられます。たとえば、身長と体重の相関などの場合です。
−1≦r≦+1 の数値で、r=0のときに無相関、プラスの時に正の相関、マイナスの時に逆相関があるというわけです。ここでサンプルから計算する相関係数(標本相関係数)をrで示し、母集団における母相関をρ (ロー) で示します。
こうした相関を計算させるときには、多くの場合、自動的に「無相関検定」が行われています。
- 帰無仮説H0: 母集団相関ρ(ローと読みます)は0である。
- 対立仮説H1: 母集団相関ρは0ではない。
多くの場合、サンプルから掲載される標本相関係数は0ではなく、それなりの相関が確認されることが多いため、相関係数がある程度の大きさで、また、データ数がある程度の大きさになっている場合は、この無相関検定は、有意水準α=0.05 などにおいて有意となり、「相関がない」という帰無仮説は棄却されることになります。
さて、そうした相関では、実際の研究に先立ってどの程度のデータ数があれば良いのかについて、事前の検定力分析で調べてみます。[α ES(Effect Size 効果量) 1-β(検定力) ] の三つを設定して、残りの変数である[データ数N]を算出するわけですが、α=0.05 などとして、 検定力としてはJ.Cohenの慣例にしたがって、 1-β=0.8 などとします。(1-β=0.7などでは、第二種の誤りの確率であるβ過誤が大きくなりすぎる、とJ. Cohenは指摘していましたね。)
残った効果量 (ES: Effect Size)ですが、J. Cohenは相関係数r の大きさそのものを用いて以下のように設定しています。すなわち―
- 「効果量 小 Small では r = 0.10」
- 「効果量 中 Medium では r =0.30」
- 「効果量 大 Large では r = 0.50」
* 効果量ESについては、ES=r と表記したり あるいは ES=|ρ| と表記することがあります。前者は標本相関係数のr で表示していますが、厳密には母相関係数であるρを用いて後者のように書くことが多いです。ρの絶対値をとり、例えば |ρ|= 0.345 等としているのは、−0.345でも+0.345でも、符号は違ってもどちらも同じ効果量だからです。
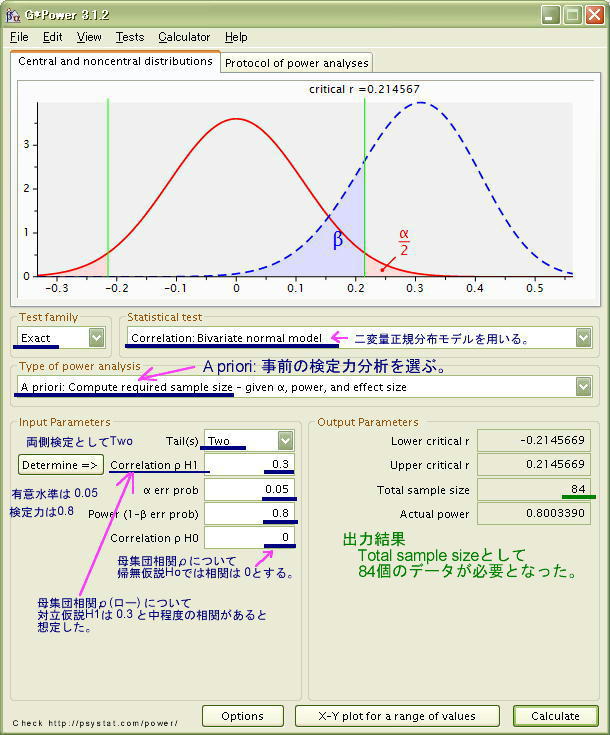
以下のG*Powerの表示では、「両側検定 Two Tails」として、「母集団相関ρ=0.3」と設定することで「効果量が中 Medium」としています。「α=0.05 」と有意水準を 5% と設定しています。また、検定力(1-β)は 0.8 と、J.Cohenの慣例を用いています。
なお、最下行の設定項目「Correlation ρ H0」とは、帰無仮説において「母相関ρ=0.0」としていることを明示しています。(母相関が0ではない特殊な場面でも計算するために数値が入力できるようになっていますが、通常は 0です。)
[Calculate]をクリックすると、右側のOutput Paremeters に結果が表示されます。 Total sample sizeが求める数値で、ここでは「 84 」となり、相関係数が0.3 といった中程度の相関がある場合にそうした結果を有意水準 5% で得るためには、「データ数は84 必要である」と算出されました。
- 相関係数についての事前の検定力分析をJ.Cohenの表2から考えてみます。
|
有意水準:α=0.05 及び 検定力:(1-β)=0.80 と設定 |
| 効果量 ES |
Small ( r = 0.1) |
Medium ( r = 0.3) |
Large ( r = 0.5) |
| 2. Sig r |
783 |
84 |
28 |
* J.Cohen(1992)の表2から抜粋。「2. Sig r」とは、表2の二番に掲載されている相関係数についての検定力分析の意味です。データ数Nの数値は、G*Powerによる結果、及び豊田秀樹『検定力分析入門』(p.122)と比べて、度数に ±1 程度のズレがあります。
この表から分かるように、相関(効果量Large)が0.5 ほどと強い関係がある場合は、検定力を0.8 と高めに設定しても、データ数が 28 もあれば、有意水準 5% で有意となる結果が得られることが分かります。(検定力=0.8 とは、相関についてのそうした研究を繰り返して実施したとすると、おおむね10回中8回程度得られることを意味します。)
臨床心理学では、ロールシャッハ・テストやMMPIなどのように、実施にかなりの時間と手間暇がかかる検査があります。そうした労力と時間の制約のためにたくさんのデータがとりにくい検査法を用いた研究でも、「中程度Mediumの効果量 0.3」すなわち、相関係数が0.3 程度の「弱い相関」ならば、データは何と! 84人分 も必要となることを示しています。
* ちなみに、相関を研究していて「有意水準α=0.05 効果量(相関係数)=0.30 データ数N= 43 」といった結果が得られた研究があったとします。検定力の事後の分析(Post hot analysis)によれぱ、「検定力(1-β)= 0.5071」と算出されます。つまり、検定力はほぼ50%程度、つまり、こうした結果は二回に1回得られる程度ということなので、この研究からは強い結論を主張するのは無理だと言うことが分かります。このように、データ数の不足が問題であることが明確に示されるので、せっかく行った研究が最初から強い主張のできないものでは困ります。したがって研究の設計段階において検定力分析を用いた検討が重要となるわけです。
|

