|
[更新 6/25, 2011]
「χ2検定」の検定力分析(1) ― 適合度の検定について
|
■ 適合度の検定 事前の分析χ2検定による検定がどの程度の「検定力」をもっているかを分析します。最初に、1行3列のデータについて「適合度検定」の場合を示します。 * 2行3列などのクロス表データについて、行と列の変数が互いに独立であるかどうかの「独立性の検定」の場合はこちらです。 適合度検定では、例えば、3つのセルの度数データ(10,30,20)について、それらが本来は「均等」であり、したがって(20,20,20)となるはずであるという仮定の下に検定を行います。つまり、帰無仮説は「20,20,20と均等である」vs. 対立仮説「(実際の度数データ 10,30,20 が示すように)3つの度数は異なっている」と想定していることになります。適合度のχ2検定では、こうした2つの仮説の対比に基づいて「均等なデータ」vs.「実度数」を用いた計算が進められていきます。(なお、「度数が均等ではないこと」が確認されるだけで、実度数のようなパターンの偏りがあることが確認されるのではありません。)
χ2値=(10-20)・(10-20) /20 + (30-20)・(30-20) /20 + (20-20)・(20-20) /20 = (100)/20 + (100)/20 + (0) / 2 = 5 + 5 + 0 = 10.0 自由度 df=(3-1)= 2 のχ2分布から、χ2=10.0となるp値は「0.0067」 ** となり 1%水準で有意となる。 上のようにすでにデータが出てしまっていますが、まずはこうした「適合度のχ2検定」について、事前の検定力分析を行って、必要なデータ数を割り出してみます。  χ2検定の「効果量 ES (Effect size)」は、J.Cohenによって、次の式で提示されています。 そして、ω=0.1 (効果量 小 Small)、 ω=0.3 (効果量 中 Medium)、 ω=0.5 (効果量 大 Large)、 となっています。 ・効果量ωとは、帰無仮説と対立仮説とのズレの程度なので、「実度数データ」が「仮定された均等度数」」からどの程度ずれているかを示す指標となっています。ここでは、効果量を 0.5 (大 Large)と設定して、大きなズレを確認するためにどの程度のデータ数Nが必要なのかを調べていきます。 ・検定力Powerは、J.Cohenの慣例に基づいて、0.8 と設定しています。自由度は (3-1)=2 となります ・有意水準は0.05、 5% としています。 右下の[Calculate]をクリックすると、Total sample size が「39」 と計算されました。つまり、効果量が「大」と実度数が大きくずれている場合は、データ数が 39 以上であれば、有意水準 5% で有意となる確率が 0.8 となることが分かったのです。 ここで検定力Power=0.8とは、こうした研究を何度も繰り返すと、10回中8回程度は「5%で有意」となる結果が得られるということを表しています。ということなので、実際の研究では、データ数Nを39以上とることにしました。そして、すでに述べたようにデータ数=60 を確保したとして、以下では「事後の検定力分析」の例を示すことにします。 ●ここにJ.Cohen (1992)の表2から、χ2検定において必要とされるデータ数Nについて抜粋しておきます。
この表は、適合度検定の場合も独立性の検定の場合も共通です。入力として異なるのは自由度のみで、行をr 列をc とすると、1行4列のデータの場合の自由度dfは (c-1)なので (4-1)=3、2行4列のクロス表データの自由度 dfは(r-1)x(c-1)なので (2-1)x(4-1)= 1x3=3 となります。 G*Powerソフトで計算した結果と、J.Cohenの表2の結果は一致しています。上で用いた例についてみると、「検定力=0.8 有意水準=0.05 自由度=2 効果量= 0.5 (Large)」としたときに必要なデータ数Nは「 39 」と同じになります。 なお、必要なデータ数Nの数値には少数点以下の丸めの誤差があるため、±1 程度のずれが起きる可能性があります。 * α=0.05、自由度df=5、効果量ES=0.1(Small)に必要なデータ数は「1293」となっていますが、G*Powerによる計算では「1283」となるので、J.Cohenの数値は誤植の可能性があります。 ■適合度の検定 事後の分析ここでは、上に示した1行3列のデータで、データ数 60の結果について、事後の分析をして「検定力」がどの程度あるのかを調べてみます。入力する必要があるのは、「有意水準 α=0.05」「実際のデータ数 60」「自由度 2」そして、「効果量ω」です。効果量ωに「小・中・大」の数値、「0.1 0.3 0.5」のどれかを暫定値として入れても良いのですが、G*Powerでは実際のデータを用いて効果量を算出できます。実際の効果量を入れる方が誤差が少ないので、ここではG*Powerの計算パネルを表示させ、そこで計算を行い、得られた効果量の数値を用いてこの研究の「検定力」を調べてみることにします。 * G*Powerの画面の中の[赤枠]の部分をクリックすると説明が一番下の説明欄に表示されます。
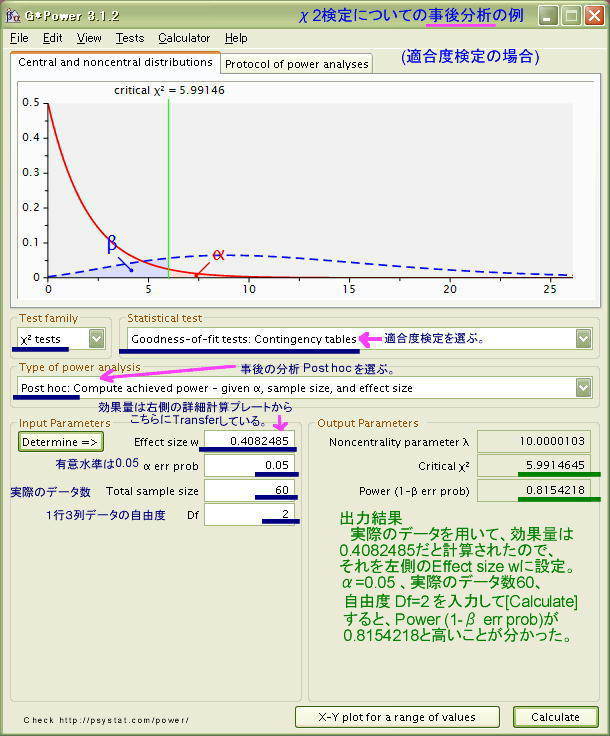 左側の入力欄に次のように入力します。 ・Effect size w は 「0.4082485」とすでに転送されて入力済みです。 ・α err prob の有意水準は、 0.05 としておきます。 ・Total smaple size には、実際のデータ数 60 を入力します。 ・Df 自由度は (3-1)= 2 なので 2 と入力します。 準備ができたので、右下のボタン[Calculate]を押します。 すると、5%で有意になるためのχ2= 5.991 と計算されました。 また、その下に求めている「検定力 Power (1-β err prob)」が 「0.8154218」と算出されました! 検定力 Power = 0.8154 という高い数値は、この実験研究を10回繰り返して行うと、そのうち8回程度は同様に有意な結果が得られることを指し示しています。ということで、60人の被調査者を用いたアンケート調査は、高い検定力(0.8154)をもつ妥当な研究となっていたことが確認されました。なお、被調査者総数が60名、三つのグループには平均すればそれぞれ20名程度と、被調査者総数がそれほど多くはない研究だったにもかかわらず、こうした高い検定力が得られたのは、ひとえに「効果量 Effect Size」が 0.4082 と大きかったこと、すなわち、三つのグループに該当する人数に相当に大きなバラツキがあったからといえます。人数{10人,30人,20人}=比率{0.166, 0.500, 0.333} |
|||||||||

