■ ２要因分散分析の事前の分析
- 多要因の分散分析とは、複数の要因があり、それぞれの要因に複数のグループ(水準・群)があるとき、各グループ毎の平均値が有意に異なっているかどうかについて、それぞれの要因ごとに分析するものです。
説明のために例えば「要因Ａ：年代1,2,3,4,5」と｢要因Ｂ：地域1,2,3」で不安耐性について調べたとします。不安耐性の平均値が五つの年代のグループ（5水準、自由度df=(5-1)=4）と、三つの地域のグループ（3水準、自由度df=(3-1)=2）の要因によって異なるのかどうか、ということがこの「２要因分散分析」の目的となります。
このとき、事前の検定力分析は、｢要因Ａの分析に必要とされるデータ数」と｢要因Ｂの分析に必要とされるデータ数」、そして｢要因Ａと要因Ｂとの相互作用の分析に必要されるデータ数」の三つの数字を別々に調べていくことになります。
検定力の事前の分析では、必要なデータ数Ｎを調べるために、[有意水準α、 効果量ES、 検定力(1-β)]の三つの数値を設定する必要があります。ここでは、これまでの経緯からとりあえず有意水準αは0.05 (5%)と設定します。検定力Powerは、J.Cohenによる慣例で(1-β)=0.8 と設定しておきます。そうすると、最後に残るのが「効果量 ES: Effect size」となります。この効果量を求めて三つの数値が出揃うことで、「必要とされるデータ数」を事前に割り出すわけです。
J.Cohen(1992)では分散分析における効果量ES(Effect Size)をｆで表示して、効果量小(Small) ｆ=0.1、 効果量中(Medium) ｆ=0.25、 効果量大(Large) ｆ=0.4」を慣例(convention)としています。なお、この効果量の数値は一元配置の分散分析の場合と同じものです。
* 効果量の式(母集団における効果量)は以下のように示されています。
- ｆ＝σm／σ
（σmは要因の標準偏差。σは母集団の標準偏差）
実際のデータを用いて算出する標本効果量の式では、偏相関比(partial correlation ratio)を用います。
- f ＝√ [(偏相関比の二乗)／(１−(偏相関比の二乗))]
- このあたりの数値の意味や実際の計算方法については豊田秀樹『検定力分析入門』に詳しく説明されているのでそちらを参照してください。
- 多要因の分散分析で必要なデータ数を事前に割り出すために、G*Powerを用いて算出するとき、次の数値が必要となります。すでに示した三つの数値を含めて書いておきます。すなわち―
- 効果量 Effect Size ｆ＝ 0.1 (効果量小)、または ｆ＝0.25 (効果量中)、または ｆ＝0.40 (効果量大)
- 有意水準 α err prob(α過誤) α＝0.05 または0.01など
- 検定力 Power (１−β err prob) power=0.80 (J.Cohenが提唱する数値)
- 要因の自由度 (Numerator df)
上の例の要因Ａの分析に必要なデータ数を割り出すときは Numerator df = (5-1)=4 とする。
上の例の要因Ｂの分析に必要なデータ数を割り出すときは Numerator df = (3-1)=2 とする。
要因Ａと要因Ｂの交互作用の分析に必要なデータ数を割り出すときは Numerator df = (5-1)x(3-1)=8 とする。
- * Numeratorは「分子」の意味で、Ｆ検定において分子に「要因の平均平方和」を入れることから来ている。
- グループの数 Number of groups
上の例では、5水準×3水準＝15となり、全部で15個のグループがあるので 15 とする。
要因の自由度を「Numerator df=4 」として要因Ａの分析に必要なデータ数を事前に算出した場合のG*Powerの画面を以下に示します。
なお、要因Ａの効果はあまり大きくないと推測されたとして、効果量f (effect siz) = 0.1 と設定しています。
要因Ａ(５水準)と要因Ｂ(３水準)の２要因分散分析ですが、要因Ａの検定力がPower=0.8となるために必要なデータ数は「Total sample size 1199」(緑色の下線)と算出されました。
全部で5x3=15個のグループがあるので、「1199÷15＝79.9」。すなわちそれぞれのグループのデータ数は「80」以上必要だということになります。
なお、効果量f=.25 と中程度の効果が推測されたとしてあらためて計算すると、Denominator df = 182、Total sample size = 197 となります。197÷15= 13.13 なので、15個それぞれのグループのデータ数は「14」以上あれば良いことが分かります。
効果量「中」(f=0.25) とは、要因Ａについてみると、5個のカテゴリーの平均値が相互にある程度異なっているという状態を意味します。したがって、データ数がそんなに多くなくとも良いということが示されているわけです。ちなみに，効果量大 (f= 0.4 )のときに必要なデータ数(Total sample size) = 81 と表示されるので、15個のグループ毎ではそれぞれ「5.4 」(81÷15)、すなわち6個程度のデータ数が良いというわけです。５個のカテゴリーの平均値が相互に極めて大きく異なっているためです。
続いて、要因Ｂについての検定力を分析してみます。
効果量f=0.1 と小さいとして、要因Ｂの自由度「Numerator df = 2」と入れて[Calculate]をクリックすると「Total sample size= 967」となります。967÷15=64.4なので、１グループ当たり65人以上必要と分かります。
最後に、要因Ａと要因Ｂの交互作用について検定力を分析してみます。
要因Ａと要因Ｂの相互作用については、「Numerator df」の欄に「 8 」と入れて[Calculate]をクリックすると「Total smaple size = 1511」となるので、１グループ当たりに必要なデータ数は「101｣人以上必要となります(1511÷15=100.73)。
このように要因Ａ、要因Ｂ、要因Ａx要因Ｂの交互作用の三つについてそれぞれ｢事前の検定力分析」を行います。この例でも分かるように、要因Ａ、要因Ｂ、要因Ａx要因Ｂの交互作用の三つの効果を知るためには、必要なデータ数がそれぞれに異なることがほとんどです。ここでは効果量ｆ= 0.1 と小さくしているため、必要なデータ数がかなり多くなっているにしても、交互作用の分析においてもPower=0.8 と高い検定力を確保するためには、合計で1511人以上の被験者を用いて研究を進めることになります。
なお、要因Ｂに最も関心があって要因Ａや交互作用はあまり気にならないような事情があれば、少なくとも要因ＢのＦ検定の結果についての検定力が高ければ良いわけです。その場合は合計で965名以上と、少し少なめの被験者数に設定するという研究設計が考えられます。(要因ＡとＡxＢの交互作用の検定力は0.8 よりも下回ってしまうことが予想される)
- G*Powerソフトによる｢必要なデータ数」の傾向について
豊田秀樹『検定力分析入門』(2009)にある例を参考にしつつ、J.Cohen(1988)の数表や解説を読んでいるのですが、算出される数値には若干のズレがあります。「必要なデータ数」を各グループ毎に見てみると、たかだか1〜2程度のズレですが、G*Powerソフトでは、「各グループ毎の必要データ数」は豊田が示している例よりもだいたい「−1」程度、少し小さな数値になる傾向があります。
これは小数点以下の計算誤差や四捨五入、切り捨てなどによる処理の違いと思われますが、G*Powerでは「Total sample size｣合計のデータ数として表示されるため、｢各グループ毎のデータ数」を表示するJ.Cohenの数値や豊田(2009)の数値との食い違いが大きく見えるためかなり気になります (G*Power3.1.2版のソフトでは、検出力の数値について小数以下四桁の精度を保つため近似計算を行わないとされています)。
見た目ほどの大きな食い違いはないようなので特に問題ないと思いますが、豊田(2009, p.193)の例を取り上げて、要因Ａ(6水準)×要因Ｂ(2水準)の場合に、「データ数」の数値のズレについて比較を示しておきます。
* 豊田(2009: p192)では、多要因分散分析について「本章では数値の繰り下げによって、任意の検定力を満たさない標本数を返す可能性を考慮して、数値の繰り上げ処理を一貫して利用する」と書かれています。
要因Ａ(6水準)×要因Ｂ(2水準)の２要因分散分析の事前の検定力分析
必要なデータ数の算出
(大きな数字が合計データ数。括弧内が12個ある各グループ毎のデータ数)
| 要因Ａについて： 自由度df=5 合計グループ数12 |
|
効果量Small f=0.10 |
効果量Medium f=0.25 |
効果量Large f=0.40 |
| 豊田(2009) p.193 |
1296 (108) |
228 (19) |
96 (8) |
| G*Power3.1.2版 |
1289 (107.4) |
212 (17.6) |
87 (7.2) |
同様に要因Ｂ(2水準)についても、必要とされるデータ数」について豊田(2009)とG*Power3.1.2の数値を対比しておきます。
* 交互作用の自由度は df=(6-1)x(2-1)=5 となるので、結果的に要因Ａについての検定力分析と同じ「必要なデータ数」となる。
要因Ａ(6水準)×要因Ｂ(2水準)の２要因分散分析の事前の検定力分析
必要なデータ数の算出
(大きな数字が合計データ数。括弧内が12個ある各グループ毎のデータ数)
| 要因Ｂについて： 自由度df=(2-1)=1 合計グループ数12 |
|
効果量Small f=0.10 |
効果量Medium f=0.25 |
効果量Large f=0.40 |
| 豊田(2009) p.193 |
804 (67) |
144 (12) |
72 (6) |
| G*Power3.1.2版 |
787 (65.5) |
128 (10.6) |
52 (4.3) |
- 多要因分散分析の「事前」の検定力の分析ですが…
多要因といっても、たかだか2〜3個の要因での研究がほとんどです。また、それぞれの要因の水準数もせいぜい2〜3から多くとも5〜6個もあればというところです。理由は単純で、要因の数と各要因内の水準の数が多いと、それらの掛け算によって、必要なグループ数が多くなってしまう―。そして、それぞれのグループに必要な被験者数、被検査者数をそろえるのが容易なことではない―。
そうした実際の状況を見ると、一般的に行われる多要因分散分析について、実はG*Powerを用いて厳密に｢必要データ数」を個々に計算するまでもなく、例えば豊田(2009)が示しているような事後分析などの例を見るだけで、必要なデータ数などはだいたい推測されることになります。なお、水準数が5〜6と多い場合や三要因以上の場合は実際に計算して確認してみることになります。
|
■ ２要因分散分析の事後の分析 (Post hoc analysis)
- 事後の検定力分析では、効果量をきちんと計算してから行う場合と、J.Cohenが示した慣例(convention)にしたがって、効果量小(Small) f=0.10、効果量中(Medium) f=0.25、効果量大(Large) f=0.40、という数値のどれかを入れて概略的に検定力を算出する場合とがあります。
先の事前の分析で用いた例を再び取り上げてみます。すなわち、「要因Ａ：年代1,2,3,4,5」(df=(5-1)=4)と｢要因Ｂ：地域1,2,3」(df=(3-1)=2) で不安耐性について、例えば、年代×地域＝5x3=15個のグループ(cell セル)のデータ数(Sample size)がすべて20人だったという場合で、全データ数(Total sample size)は15x20=300となります。
このように研究が行われた場合、「事後 post hoc」に、要因Ａ｢年代」の検定力を算出してみます。
- [Test family] F tests
- [Statistical test] ANOVA] Fixed effects,special, main effects and interactions
- [Type of power analysis] Post hoc: Comute achieved power - given α, sample size, and effect size
Input Parameters
- [Effect size f] 0.25
(実測値を用いず「効果量は中くらい」だと想定した)
- [α err prob] 0.05 (有意水準は5%)
- [Total sample size] 300 (全データ数 5x3x 20名)
- [Numerator df] 4 (要因Ａ｢年代」の自由度df= 5-1 )
- [Number of groups] 15 (グループの総数 5x3)
この結果は下の図をご覧下さい。
Output Parameters
- [Noncentrality parameter λ] 18.7500000 (非心分布のλパラメータの値
- [Critical F] 2.4033200 (5%水準で有意となるためのＦ値)
- [Denominator df] 285 (誤差の自由度: (20-1)x15グループ=285)
- [Power (1-β err porb)] 0.9484892
|
これにより「要因Ａ：年代(5水準)」についての有意性検定の検定力は「0.9484」と極めて高いことが計算されました。
- ２要因分散分析の事後の検定力分析に実際の効果量を用いる。
ところで、研究が終わった後では、｢効果量 中 f=0.25」と勝手に入れてみるのではなく、実際のデータに基づいた効果量(Effect size)を入力して正確な検定力を知りたいわけです。
必要なのは分散分析表に載っている次の３項目です。あらためて別の例として要因Ａ(グループ数３)についてみると…
- 「要因Aの自由度 dfA 」 水準数が3ならば (3-1)=2
- 「要因AのＦ値 FA 」 分散分析表に載っている数値
- 「誤差の自由度 dfe 」 誤差(Error)の自由度
たとえば、次の数値だったとします。
- 「要因Aの自由度」 dfA = 2
- 「要因AのＦ値」 FA = 20.5205
- 「誤差の自由度」 dfe = 84
以下の計算式は既出の豊田(2009)に掲載されています。最初に要因Ａの「偏相関係数 η2」(イータ二乗)を計算し、その値を用いて｢効果量 f 」を計算します｡
- ・偏相関係数 η2＝ dfA x ＦA ／ (dfA x ＦA + dfe)
偏相関係数 η2＝ 2 x 20.5205 / (2 x 20.5205 + 84) = 41.041 / 125.041 = 0.3282203
- ・効果量 f ＝ √ (η2／(1 −η2))
効果量 f ＝ √ (0.3282203 / (1 - 0.3282203 ) = √ (0.3282203 / 0.6717797 ) = 0.6989872
ということで｢効果量 f = 0.6989872 」ということが分かりました。この効果量はかなり大きな値で、J.Cohenが示した効果量大 (Large) f=0.40 よりも大きいものです。したがって、検定力もかなりの高さになるだろうと期待されます。
- 分散分析表のＦ値を用いて計算する
一要因分散分析でもＦ値から効果量を計算する電卓ソフトを紹介しましたが、二元配置でも同じく使えますので紹介いたします。
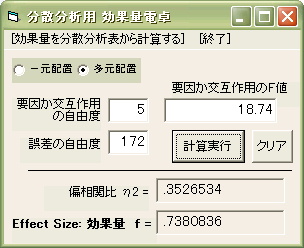まず、「多元配置」(多要因分散分析)を選びます。
一例として表示している数値は、Ｆ( 5, 172) = 18.74 という分散分析表からのものです。要因の自由度 5、誤差の自由度 172、そして要因のＦ値= 18.74 ということを示す表記から、この効果量電卓に入力して「計算実行」を押すと、偏相関比 η2 = .3526534 と 要因の効果量 f = .7380836 が表示されます。
*他の例として Ｆ( 2, 84) = 20.5205 の場合は、この効果量電卓で計算すると
偏相関比 η2 = 0.3282203、要因の効果量 f = 0.6989874となります。(小数点以下４桁以下あたりから計算誤差)
※この効果量電卓は上に示した計算式を用いてるので、一要因、２要因、３要因などの場合も同様に使用できます。
●得られた効果量を検定力分析ソフト G*Power に入力して、その要因(あるいは交互作用)の検定力を知ることができます。これまでに発表された論文の分散分析の結果について、どの程度の検定力があるかを調べることができます。
検定力が低い場合、少なくとも、1)各グループの平均値に大きなズレがないこと、2)各グループ毎のデータ数が不足していること、の２つの場合が考えられます。1)の場合は平均値のズレが大きく効果量が大きくなるような研究を考える必要があるでしょう。また、2)の場合はデータ数を多くした研究を考えなければなりません。この1)2)を踏まえて現実的な研究設計を行うことによって、内容のある研究を実施することが可能となるでしょう。
|
